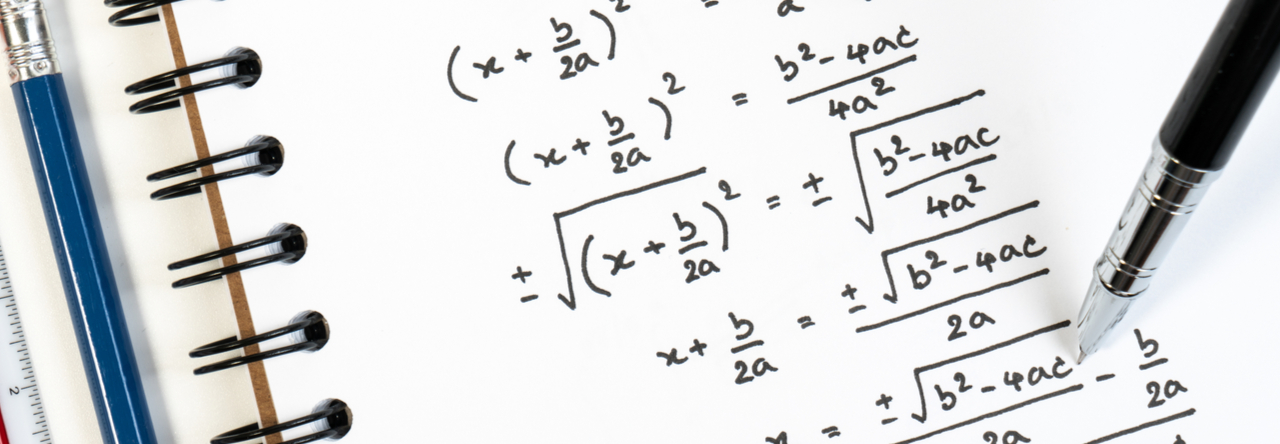What is algebra? Basically in its simplest form, a simple algebraic equation just uses a letter (usually X) which stands for something we don’t know – but we do know that if we do something mathematical to it, we get a number.

A very simple example

X + 1 = 2

So we have our unknown variable (a variable is something that can change) and we know that if we add 1 to it, we get 2.

The ‘=’ sign just means ‘is equal to’. I sometimes teach this as ‘balances’.

There are lots of ways of solving this – and there is no single correct way. All ways are valid as long as they get you the correct result. Personally, there is too much focus on the right method. I believe that it’s the result and understanding how you get there that’s important.

The function machine approach.

In our machine, there is a single step.

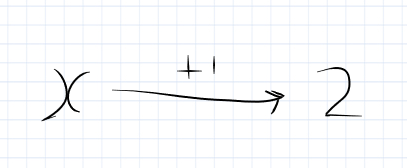
X goes in, we add 1 to it, we get 2. So to ‘undo’ it, we have to work backwards. So the first thing we do is subtract 1 from 2. This gives us 1. So X = 1

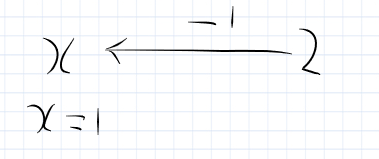
The seesaw approach

On one side of the seesaw, you have X + 1 and on the other side, you have 2. In order to get X by itself on one side, you have to do the same thing to both sides.

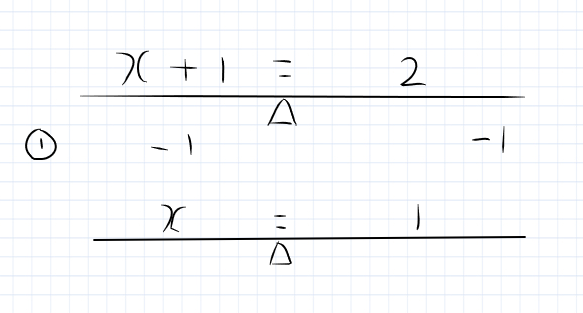
So you take away 1 from both sides. This leaves X on 1 side and 1 on the other side. So X = 1

‘Plugging it back in’

You can check you’re right by ‘plugging’ the answer back in the equation.

In the equation X + 1 = 2 , let’s replace X with 1. Does 1+ 1 = 2? Yes!!

So it works!

Making it harder

3X + 5 = 20

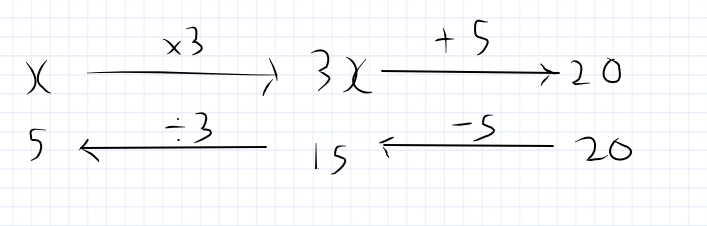
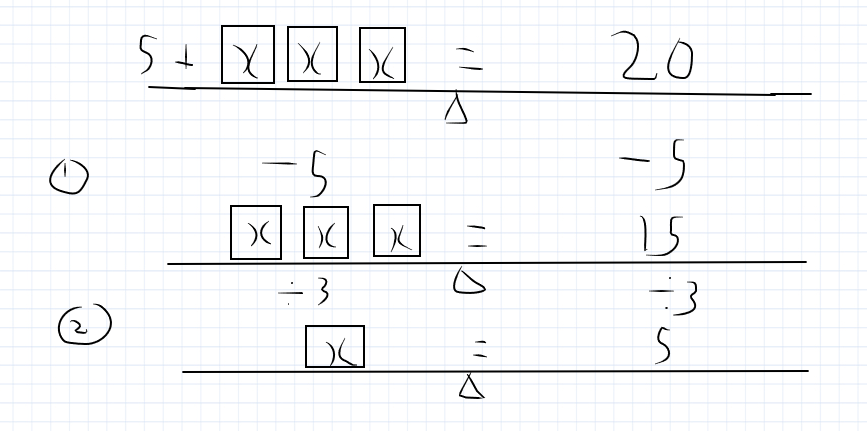
So the answer is X = 5. If you plug that back into your equation, 3 x 5 + 5 = 20

So it’s correct!

The basic concept is undoing the equation to get ‘X’ by itself. The key thing is the ability to read the equation and to understand the inverse (the opposite) function. You also need to know the order of the operations.

Once pupils understand the idea of ‘undoing’ or doing the same thing to both sides, this helps in their tackling of algebraic problems. It also has lots of applications in real life maths problems where you can simply use ‘X’ to solve a problem.

e.g.

Sam is 5 years older than Bob. Their total age is 35. How old are Sam and Bob?

We could say that Bob is X years and Sam is X + 5 years old.

Their combined age is X + X + 5 which is the same as 2X + 5.
This is equal to 25
So we know that 2X + 5 = 35.

Solving using either of these methods gives the result that X = 15
So Bob is 15 years old and Sam is 20 years old.

Algebra can be hard for some pupils and there are a range of different approaches to it. Some pupils like to use visual techniques and I am highly experienced in using those approaches. If you live in the York area and you are looking for an experienced tutor, then please contact me.